Notion de tenseur de contrainte à trois dimensions

Notion de tenseur de contrainte à trois dimensions

Nous considérons en première abord dv un volume infiniment petit. Examinons les forces qui s’exercent sur ce volume. Il y a équilibre des forces entre :

Le poids de l’élément et s’il y a mouvement ou vibration la force d’inertie. Les deux quantités sont proportionnelles à dv, donc du 3ème ordre (dimension d’un volume).

Les forces de tension qui s’exercent sur la surface limite. Ces forces sont proportionnelles à ds, donc du 2ème ordre (dimension d’une surface). Les forces de volume sont donc d’un ordre supérieur par rapport aux forces de surface, donc, dans ce raisonnement portant sur des quantités infiniment petites, les forces de volume sont négligeables par rapport aux forces de surface.

Pour qu’il y ait équilibre, il faut que les forces de tension s’équilibrent entre elles. Ceci posé, on peut ainsi écrire la première condition d’équilibre :

Soit dv le tétraèdre OABC dont les trois faces forment un trièdre orthogonal (figure ci-dessous). Soit ν le normale extérieure à ABC, on a :

Aire ABC = S

BOC = S_x = S cos(ν, ox)

COA = S_y = S cos(ν, oy)

AOB = S_z = S cos(ν, oz)

Cette figure illustre la notion de tenseur des tensions en O. Le vecteur tension dépend de l’orientation de la normale à la surface élémentaire ABC. Il faudra donc trois vecteurs et leurs neuf composantes cartésiennes pour le définir complètement. Source@ Geophysique.

Si l’on remarque que BOC a −x pour normale extérieure et que τ(−x) = −τ(x), la première condition d’équilibre s’écrit :

τ_νS − τ_xS_x − τ_yS_y − τ_zS_z = 0

où,

τ(ν) = τx cos(ν, x) + τy cos(ν, y) + τz cos(ν, z)

Il en résulte que τ_ν est connue pour toute direction ν dès que l’on se donne les 3 tensions particulières τ(x), τ(y), τ(z).

Cette association en un point du corps, d’un vecteur τ_ν à toute direction suivant une « relation linéaire et homogène par rapport aux cosinus directeurs de ν traduit le concept général de tenseur ».

On dit que τ_ν est la composante du tenseur des tensions suivant la direction ν. Les 3 composantes des 3 vecteurs qui définissent le tenseur sont :

τ(x) τxx τxy τxz

τ(y) τyx τyy τyz

τ(z) τzx τzy τzz

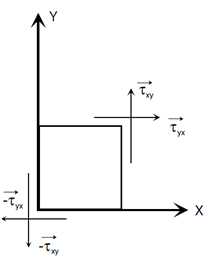
Pour la deuxième condition d’équilibre on considère un volume infinitésimal en forme de cube dont les arêtes sont parallèles aux axes Oxyz (figure ci-dessous).

Cette figure illustre la nullité du moment par rapport aux axes de coordonnées permet de ramener à six, grâce aux propriétés de symétrie, le nombre des paramètres nécessaires pour définir le tenseur des tensions. @Geophysique.

Le moment par rapport à OZ des forces de tension provient des forces±τyx dS et ±τxy dS qui s’exercent sur les 4 faces du cube. Ce moment est nul si τxy = τyx. Par un raisonnement identique on a τzy = τyz et τxz = τzx.

Ainsi, le tenseur des tensions est symétrique. Sa matrice admet une diagonale comme axe de symétrie. Il suffit donc de six nombres et non de neuf, pour définir complètement le tenseur des tensions.

<<< Notion de tension         Retour aux notions fondamentales de la sismologie >>>